回归
回归模型根据包括特征和已知标签的训练数据来预测数值标签值。 训练回归模型(或事实上,任何监督机器学习模型)的过程涉及多个迭代,在该迭代中使用适当的算法(通常具有一些参数化设置)来训练模型、评估模型的预测性能,并通过使用不同的算法和参数重复训练过程来优化模型,直到达到可接受的预测准确性级别。
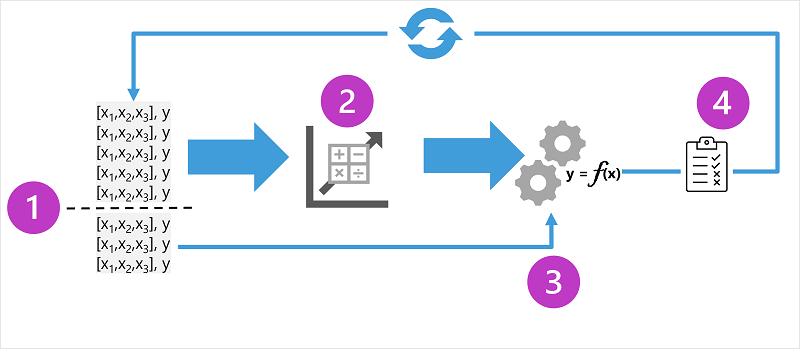
此图显示了用于监督机器学习模型的训练过程的四个关键元素:
- 拆分训练数据(随机)以创建一个数据集,用于训练模型,同时保留用于验证已训练模型的一部分数据。
- 使用算法将训练数据拟合到模型。 对于回归模型,请使用回归算法,例如 线性回归。
- 使用你保留的验证数据通过预测特征的标签来测试模型。
- 将验证数据集中的已知 实际 标签与模型预测的标签进行比较。 然后聚合 预测 标签值与 实际 标签值之间的差异,以计算指示为验证数据预测的模型的准确性的指标。
每次训练、验证和评估迭代后,都可以使用不同的算法和参数重复该过程,直到达到可接受的评估指标。
示例 - 回归
让我们通过一个简化的示例来探索回归,在此示例中,我们将训练模型,以基于单个特征值(x)预测数字标签(y)。 大多数实际方案涉及多个特征值,这增加了一些复杂性;但原则是相同的。
对于我们的示例,让我们坚持前面讨论的冰淇淋销售方案。 对于我们的功能,我们将考虑 温度 (假设该值是给定日期的最高温度),我们要训练模型预测的标签是当天销售的冰淇淋数量。 我们将从一些历史数据开始,其中包括每日温度(x)和冰淇淋销售记录(y):

|

|
|---|---|
| 温度 (x) | 冰淇淋销售(y) |
| 51 | 1 |
| 52 | 0 |
| 67 | 14 |
| 65 | 14 |
| 70 | 23 |
| 69 | 20 |
| 72 | 23 |
| 75 | 26 |
| 73 | 22 |
| 81 | 30 |
| 78 | 26 |
| 83 | 36 |
训练回归模型
首先拆分数据并使用其中一部分来训练模型。 下面是训练数据集:
| 温度 (x) | 冰淇淋销售(y) |
|---|---|
| 51 | 1 |
| 65 | 14 |
| 69 | 20 |
| 72 | 23 |
| 75 | 26 |
| 81 | 30 |
若要深入了解这些 x 值和 y 值如何相互关联,我们可以将它们绘制为沿两个轴的坐标,如下所示:
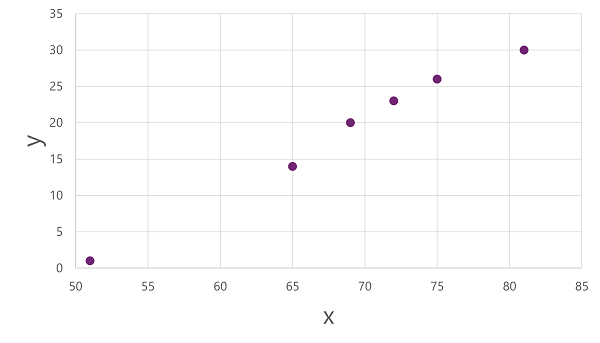
现在,我们已准备好将算法应用到训练数据,并将其拟合到将作应用于 x 以计算 y 的函数。 其中一种算法是 线性回归,它的工作原理是派生一个函数,该函数通过 x 和 y 值的交集生成直线,同时最大限度地减少线条和绘制点之间的平均距离,如下所示:
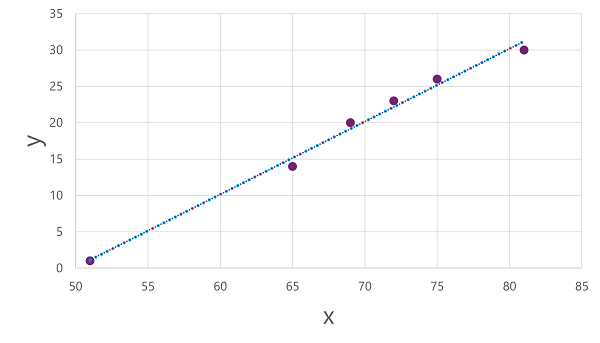
该线是函数的可视表示形式,该函数的斜率描述如何计算给定值 x 的 y 值。 线条截获 x 轴为 50,因此当 x 为 50 时, y 为 0。 从绘图的轴标记中可以看到,线条斜率使 沿 x 轴的 5 个增加会导致 5 个向上 y 轴增加:因此,当 x 为 55 时, y 为 5; x 为 60、 y 为 10 等。 若要计算给定值 x 的 y 值,函数只需减去 50;换句话说,函数可以如下所示表示:
f(x) = x-50
可以使用此函数来预测一天以任何给定温度销售的冰淇淋数量。 例如,假设天气预报告诉我们,明天将达到 77 度。 我们可以应用模型来计算 77-50 ,并预测明天将销售 27 个冰淇淋。
但是我们的模型有多准确?
评估回归模型
为了验证模型并评估其预测程度,我们保留了一些我们知道标签(y)值的数据。 下面是我们保留的数据:
| 温度 (x) | 冰淇淋销售(y) |
|---|---|
| 52 | 0 |
| 67 | 14 |
| 70 | 23 |
| 73 | 22 |
| 78 | 26 |
| 83 | 36 |
我们可以使用模型根据特征(x)值来预测此数据集中每个观察值的标签;然后将预测的标签(ŷ)与已知的实际标签值(y)进行比较。
使用前面训练的模型(封装函数 f(x) = x-50)会导致以下预测:
| 温度 (x) | 实际销售额(y) | 预测销售额 (ŷ) |
|---|---|---|
| 52 | 0 | 2 |
| 67 | 14 | 十七 |
| 70 | 23 | 20 |
| 73 | 22 | 23 |
| 78 | 26 | 28 |
| 83 | 36 | 33 |
我们可以针对特征值绘制 预测 标签和 实际 标签,如下所示:

预测标签由模型计算,因此它们位于函数行上,但函数计算的 ŷ 值与验证数据集中的实际 y 值之间存在一些差异:这在绘图上指示为 ŷ 与 y 值之间的一条线,显示预测与实际值之间的距离。
回归评估指标
根据预测值与实际值之间的差异,可以计算用于评估回归模型的一些常见指标。
平均绝对误差 (MAE)
此示例中的方差指示每个预测的错误冰淇淋数量。 预测 是否超过 或 低于 实际值并不重要(例如,-3 和 +3 都表示 3 的方差)。 此指标称为每个预测的 绝对误差 ,可以汇总整个验证集的 绝对误差 (MAE)。
在冰淇淋示例中,绝对误差(2、3、3、1、2 和 3)的平均值(平均值)为 2.33。
均方误差 (MSE)
平均绝对误差指标将预测标签和实际标签之间的所有差异都考虑在内。 但是,最好有一个模型,该模型一直错误的数量少于一个,但更大的错误。 一种方法是将单个错误与计算平方值的平均值 相等 ,从而生成“放大”较大错误的指标。 此指标称为 平均平方错误 (MSE)。
在我们的冰淇淋示例中,平方绝对值的平均值(即 4、9、9、1、4 和 9)为 6。
均方根误差 (RMSE)
平均平方误差有助于考虑误差的大小,但由于它 正方形 误差值,因此生成的指标不再表示标签测量的数量。 换句话说,我们可以说,模型的 MSE 为 6,但这并不能衡量其准确性,即被错误预测的冰淇淋数量:6 只是一个数字分数,指示验证预测中的错误级别。
如果要测量冰淇淋数量方面的误差,则需要计算 MSE 的 平方根 ;这会生成一个名为“不出所料”的指标, 即根均方误差。 在本例中,√6,即 2.45 (冰淇淋)。
确定系数 (R2)
到目前为止,所有指标都会比较预测值与实际值之间的差异,以便评估模型。 然而,实际上,模型考虑的冰淇淋的日销售额存在一些自然随机差异。 在线性回归模型中,定型算法适合一条直线,可最大程度地减少函数和已知标签值之间的平均方差。 确定系数(更常见的称为 R2 或 R-Squared)是一个指标,用于度量模型可以解释的验证结果中的方差比例,而不是验证数据的一些异常方面(例如,由于当地节日,具有非常不寻常的冰淇淋销售额的一天)。
R2 的计算比以前的指标要复杂得多。 它将预测标签与实际标签值与实际标签值平均值之间的平方差异之和进行比较,如下所示:
R2 = 1- ∑(y-ŷ)2 ÷ ∑(y-ȳ)2
如果看起来很复杂,请不要担心太多;大多数机器学习工具可以计算指标。 要点是,结果是一个介于 0 和 1 之间的值,用于描述模型解释的方差的比例。 简言之,此值越接近 1,模型就越适合验证数据。 对于冰淇淋回归模型,根据验证数据计算的 R2 为 0.95。
迭代训练
上述指标通常用于评估回归模型。 在大多数实际方案中,数据科学家将使用迭代过程重复训练和评估模型,变化:
- 特征选择和准备(选择要包含在模型中的功能,以及应用于它们的计算,以帮助确保更适合)。
- 算法选择(我们在上一示例中探索了线性回归,但还有其他许多回归算法)
- 算法参数(用于控制算法行为的数值设置,更准确地称为 超参数 ,以将它们与 x 和 y 参数区分开来)。
多次迭代后,选择可接受特定方案的最佳评估指标的模型。